Критерий силы
Труды лаборатории искусственного интеллекта Массачусетского технологического института, MIT Papers on Artificial Intellect Systems, Massachusetts Institute of Technology, Cambridge, Massachusetts, Volume XXIV, 2005, pp. 33-35
перепечатано из (**):
Труды по теории вычислительных систем Швейцарской высшей технической школы Цюриха, ETHZ Proceedings on Computer Systems, Eidgenössische Technische Hochschule Zürich, Vol. 13, 1939, pp. 21-24
К вопросу об изоморфной трансформации математических систем
Ули Тегетмайер, Дитер Виттманн
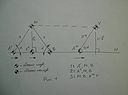
Представим себя на берегу моря тёмным вечером. Безветрие. Штиль. А теперь обратимся к рисунку.
На нём обозначены: Н – линия горизонта, М – Марс, V – предположительно – Венера (или какая-то очень яркая звезда), В – бортовой огонь судна где-то у самого горизонта, А – огонь судна, идущего слева направо вблизи берега, параллельно ему. Для наших целей принимаем, что элементы М, В и V – неподвижны (в пределах времени наблюдения и соотносительно со скоростью объекта А). Очевидно, что отмеченные элементы, с учётом явного, последовательного и равномерного перемещения судна А, будут образовывать ряд неких геометрических фигур. А теперь перейдём к существу дела.
Станем называть системой каждую правильную из сконфигурированных таким образом фигур. Вот – последовательный во времени ряд таких систем: система 1 – равнобедренный треугольник (А’, M, B), система 2 – треугольник с прямым углом (A”, M, B), система 3 – равнобедренная трапеция (M, B, A’”, V). Мы видим, что элементы М, В и А входят в состав каждой из перечисленных систем. Будем называть их сильными элементами, а последовательность фигур – не отдельными системами, а одной и той же – в разных своих воплощениях. Попутно заметим, что условием для выбора объектов, пригодных стать элементами систем(ы) явилась степень их яркости – на небосводе и на водной глади. Сформулируем ряд положений.
1) Для любой системы всегда существует как минимум один критерий, по которому можно выявить её сильные элементы. Это – критерий силы (*).
2) Системы с единственным критерием – простейшие, с более, чем одним – полиморфные. Количество критериев – степень полиморфности. Признак того, что это есть всё-таки, одна система, а не множество разных – как минимум один общий сильный элемент. Чем их больше (таких общих сильных элементов), тем сильнее система связана – тем выше её коэффициент связанности.
3) Каждый из критериев предполагает свою среду обитания системы.
4) Чем выше степень полиморфности, тем система более жизнеспособна.
У нас нет пока аргументов в пользу изложенного подхода, а именно – объединения некого ряда систем, при определённых условиях и по определённым признакам, в одну – в своих разных воплощениях. Разве что – математическое изящество такого метода. Но у нас есть стойкое ощущение, что появление более существенных аргументов (нашими усилиями или же – чьими-то другими) есть лишь вопрос времени. С нашей стороны мы приложим все усилия для сокращения этого времени, понимая, разумеется, что в такого рода вещах результат не может быть запланирован.
(*) Заметим, что в качестве примера нам достался очень интересный случай – критерием силы здесь является степень подвижности объектов, но сильными из них оказываются как неподвижные (что легко было бы предположить), так и подвижные (что неожиданно). Объяснение последнему одно – именно подвижный элемент (судно А) и обеспечивает системе ряд её последовательных воплощений – её множественность.
(**) Прим. редакции:
Мы полагали эту давнюю публикацию важной настолько, что сделали перепечатку из университетского сборника – редкого ротапринтного издания. По нашим представлениям, этот текст есть самая ранняя из известных нам предтеч появления нынешних облачных технологий и оперирования не рядом отдельных систем, а – их флуктуирующим множеством.
Игорь Савченко
Мисхор-Минск, август-декабрь 2018


























Sasha-Velichko-(1)-thumb.jpg?alt=media&token=53e8f1c7-85c7-41a9-bce4-f1cd3dd6d28c)